When Heuristics Bite Back

The day adjustable counters met a wicked unit test and lost.

Photo by Wim Arys on Unsplash

In my last update on building a logic engine with Claude Code (and GPT-5), I probably made it sound like all saxophones, all the time. It mostly is—and we’ve come a long way. But I left out one off-note “detail” that ate much of last weekend. Let’s visit it.

The core logic engine is now guarded by over 1,900 unit tests. In day-to-day development, a few fail—sometimes a lot right after a big refactor—that’s expected. Most pass most of the time, which keeps me confident we’re broadly on course. But over the past couple of weeks, something shifted from annoying to worrisome: on a small subset of tests, the reasoner would intermittently vanish into recursive rabbit holes. In those cases, memory and CPU climbed and perched there and stared back—sometimes for minutes.

It didn’t happen often—and there was plenty else going on to disguise it as a priority problem—but it kept dropping in, every now and then.

A couple of weeks ago, Claude and I implemented an expedient fix: add depth limits and loop counters to bail out of deep recursion. It worked… mostly. The timeouts stopped, but something was off—and I didn’t press, because so much else was in flux.

The problem is obvious in hindsight: if you “fix” excessive recursion by stopping, you also risk missing legitimate answers. Path-finding queries sometimes came back incomplete. Ancestor chains dropped valid links. A few unit tests failed. We’d traded correctness for throughput—a terrible bargain when you’re building a logic engine.

What’s in a heuristic? How many loops are too many? How deep is too far? Once we started that path, it became all too easy to keep patching: bump the counters, paper over the next edge case. Then, last weekend, a couple of wicked new unit tests blew it up once again.

That’s when it clicked: the “fix” was the bug.

Enter GPT-5. After a couple of hours circling the problem, I stepped back. I went for a run, then fed GPT-5 a bundle of Claude status reports from that period and asked for its assessment.

The figure below is GPT-5’s spot-on read of the core issue. What’s wild is that it was mostly an informed guess. Claude’s status reports are loquacious—megabytes per hour of high-quality Markdown—so GPT-5 had plenty to chew on, but it didn’t have source access—it wasn’t Claude with repo-level maneuverability. And still, it nailed it.

Figure 1. GPT-5’s assessment: unbounded recursion masked as ‘maybe progress’

But it didn’t stop there. Its proposed solution was also amazing (see Figure 2).

Figure 2. GPT-5’s proposed fix: tabled resolution (SLG) with variant keys.

I dropped the solution sketch (Figure 2) into Claude. It told me I was brilliant, it lept down the new path, worked out the details. We got it implemented and never looked back.

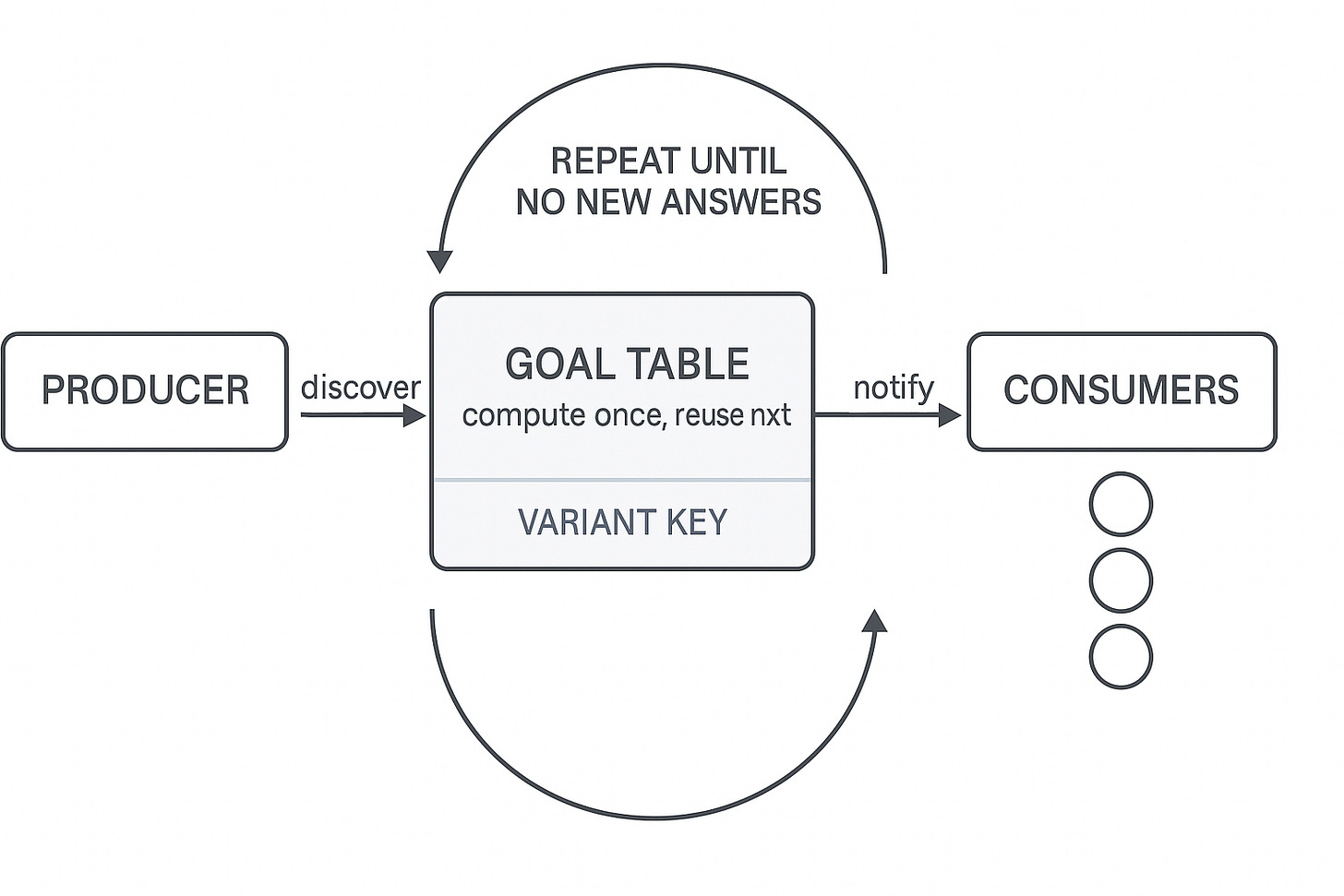
The fix was tabling: treat each goal—i.e., a predicate call/subgoal in a query like path(a, X)—as a reusable computation. On the first call, the goal becomes a producer and its answers are stored in a table keyed by a variant key (same structure with variables normalized—alpha-equivalent calls share a key). Later calls to the “same” goal act as consumers—they reuse known answers and are notified as new ones arrive. A fixpoint loop keeps the system iterating until it reaches a steady state. In practice, this eliminates infinite loops, preserves completeness on cycles and left recursion, and slashes duplicate work.

Figure 3 is a GPT-5–generated diagram that captures the core tabling idea at a glance.

Figure 3. Why tables win: reuse answers; stop recomputing.

For those who want more details, the Appendix is Claude Code’s report of how it went down.

What We (Re-)Learned the Hard Way

For starters, heuristics aren’t correctness. Tweaking depth limits and retry counters can feel like “performance tuning,” but in hindsight, we weren’t solving the recursion problem—we were negotiating with it. And problems like this don’t negotiate in good faith.

Our breakthrough came from a handful of stubborn unit tests. They kept exposing systemic flaws, and instead of working around them, I finally listened. The message was simple: adopt proven algorithms. SLG-style tabling—producer/consumer tables, variant keys, and a fixpoint loop—solved these exact problems decades ago in the logic-programming world.

Yeah, now I know and am reading up on it. Oh, and that is another lesson— you can pick up ideas from AI and learn things!

Using GPT-5 as a second set of eyes on Claude’s diagnostic reports created a productive feedback loop: AI helping me debug AI. That outside perspective quickly clarified architectural choices we’d been circling. I’m not claiming GPT-5 outperformed Claude overall—sometimes the reverse was true—but the alternate viewpoint was invaluable for triangulating on the right solution in a messy situation.

Have a great day!

---

Appendix

What follows is Claude Code’s report of last weekend’s epiphany encounter and resolution of a long-standing bug in the Prolog engine.

Chronicle: The Recursion Handling Bug and Evolution to Table-Based Solution

Executive Summary

Over the course of a couple of months, the BSF2-IF Knowledge Base system encountered a recurring, critical bug where recursion handling would work for extended periods but then fail when edge cases were encountered. The root cause was identified as a counter-based heuristic approach to managing recursive queries, which proved fundamentally insufficient for ensuring correctness. After analysis and multiple attempted fixes, the team determined that a table-based approach (SLG-style tabling) was the only long-term solution that could provide both termination guarantees and completeness for recursive queries.

This document chronicles the problem’s evolution, the insights gained, and the architectural decision to move from heuristics to a principled table-based solution.

---

The Problem: Recursion Handling with Counter-Based Heuristics

Initial Approach: Depth Counters and Cycle Detection

The original implementation used multiple counter-based mechanisms to prevent infinite recursion:

1. Depth Counter (_eval_depth): Tracked recursion depth with a hard limit (MAX_EVAL_DEPTH = 100)

2. Transitive Depth Limit (MAX_TRANSITIVE_DEPTH = 20): Special handling for transitive predicates

3. Consecutive Failure Counter (MAX_CONSECUTIVE_FAILURES = 10): Heuristic to detect infinite loops

4. Cycle Detection Set (_eval_stack): Tracked in-flight queries to detect immediate cycles

# From kb_reasoner.py (legacy approach)
class Reasoner:
    def __init__(self, ...):
        # Recursion depth tracking for evaluate_derived
        self._eval_depth = 0
        self._max_eval_depth = 100

        # Query cycle detection using canonical keys
        self._eval_stack: Set[Tuple[str, str]] = set()

Why This Seemed Reasonable

The counter-based approach appeared to work initially:

• Simple to implement and understand

• Handled most common recursion patterns

• Provided stack overflow protection

• Fast - minimal overhead

The Recurring Problem: Edge Cases Breaking the Heuristics

The bug manifested in subtle, hard-to-reproduce ways:

Pattern 1: False Cycle Detection

The cycle detection stack could incorrectly identify legitimate queries as cycles when:

• Queries had similar structure but different bindings

• Temporary eval stack state from previous queries contaminated detection

• Exclusive fluent checks triggered false positives

Evidence from code:

# kb_reasoner.py:676-689
# Workaround: Temporarily clear eval stack during exclusive fluent checks
saved_stack = self._eval_stack.copy() if hasattr(self, ‘_eval_stack’) else set()
if hasattr(self, ‘_eval_stack’):
    self._eval_stack.clear()

try:
    # Check if this event initiates an exclusive fluent
    # Don’t use cutoff_time to avoid cycle detection issues
    ...
finally:
    if hasattr(self, ‘_eval_stack’):
        self._eval_stack = saved_stack

This workaround was a red flag - the system was fighting against its own cycle detection mechanism.

Pattern 2: Depth Limits Preventing Valid Queries

For complex transitive closures (like temporal reasoning in narratives), the depth limit would be reached before all valid answers were found.

Historical evidence:

# engine/constants.py - History section
# Originally 10
# Increased to 20 to handle murder mystery narrative scenarios
MAX_TRANSITIVE_DEPTH = 20

The fact that this limit kept needing adjustment showed the heuristic was fundamentally inadequate.

Pattern 3: Consecutive Failure Heuristic Missing Valid Results

The MAX_CONSECUTIVE_FAILURES heuristic would terminate evaluation prematurely in graphs with sparse connectivity:

# engine/constants.py:98-123
# Purpose:
#   Prevents infinite loops when evaluating recursive rules with circular data.
#   When evaluating body goals against static facts, if N consecutive recursive
#   calls return empty results, stop trying additional static facts.
#
# Default: 10
#   Rationale: If 10 consecutive attempts all fail due to depth limit, it’s extremely
#              unlikely that continuing will succeed.

The phrase “extremely unlikely” reveals this is a probabilistic heuristic, not a correctness guarantee.

---

The Breaking Point: Recursive Queries Need Correctness, Not Heuristics

The Insight: Two Fundamental Requirements

After repeated encounters with edge cases, the team identified that recursive queries have two non-negotiable requirements:

1. Termination: Queries must halt, even on cyclic data

2. Completeness: Queries must find ALL valid answers, not just “most” answers

Heuristics cannot guarantee both.

Specific Failure Scenarios

Scenario A: Transitive Closure with Cycles

% Graph with cycle: a → b → c → d
%                    ↑_________|
edge(a, b).
edge(b, c).
edge(c, d).
edge(d, c).  % Creates cycle

% Query: path(a, X)
% Expected: {b, c, d} (complete transitive closure)

Counter-based result: Might find {b, c} before hitting depth limit, missing {d}.

Table-based result: Correctly finds {b, c, d} via fixpoint iteration.

Scenario B: Diamond-Shaped Dependency Graph

% Two paths from a to d:
%   a → b → d
%   a → c → d
edge(a, b).
edge(a, c).
edge(b, d).
edge(c, d).

% Query: path(a, X)
% Expected: {b, c, d}

Counter-based result: Depends on search order and depth remaining - might miss some answers.

Table-based result: Systematically explores all paths, guarantees complete answer set.

Scenario C: Mutual Recursion

even(0).
even(N) :- N > 0, N1 is N - 1, odd(N1).
odd(N) :- N > 0, N1 is N - 1, even(N1).

Counter-based result: Works for small N, fails at depth limit for larger N.

Table-based result: Handles arbitrary N (up to memory limits), no artificial depth restrictions.

---

The Decision: Adopt Table-Based Solution

Why Tables?

Tabling (SLG-style resolution) is the industry-standard solution for recursive queries in logic programming systems. It provides:

1. Intrinsic Cycle Detection: Cycles are detected naturally through variant matching, not heuristics

2. Complete Answer Sets: Fixpoint iteration ensures all answers are discovered

3. Guaranteed Termination: Producer/consumer protocol prevents infinite loops

4. Performance Benefits: Memoization eliminates redundant computation

The Producer/Consumer Protocol

The table-based approach works through a simple but powerful protocol:

1. First call to variant → Create PRODUCER
   - Producer evaluates goal, stores answers in table

2. Subsequent calls to same variant → Create CONSUMER
   - Consumer waits for producer’s answers
   - CYCLE DETECTED (returns current partial answers)

3. Producer finds new answer → Notify all consumers
   - Consumers resume with new information

4. Repeat until FIXPOINT (no new answers)
   - Mark table as COMPLETE

Key insight: Cycles are not errors to prevent - they are expected patterns that tables handle naturally.

Implementation Architecture

The table-based solution consists of three core components:

1. Variant Key System (engine/tabling/variant_key.py)

Normalizes queries to detect when two calls are “variants” (same structure, different variable names):

# path(a, X) and path(a, Y) are variants → same table entry
# path(a, X) and path(b, X) are NOT variants → different tables

Critical for: Recognizing when a recursive call is truly the same query (cycle detection).

2. Table Manager (engine/tabling/table_manager.py)

Manages the lifecycle of table entries:

class TableEntry:
    status: TableStatus  # EVALUATING or COMPLETE
    answers: AnswerSet   # All answers found so far
    waiting_consumers: List[Consumer]  # Consumers waiting for new answers

Critical for: Storing intermediate results and coordinating producer/consumer protocol.

3. Fixpoint Driver (engine/tabling/fixpoint_driver.py)

Orchestrates the saturation loop that iterates until no new answers are discovered:

def evaluate_with_fixpoint(goal_evaluator, goal, query_vars):
    # 1. Initial evaluation (creates producers/consumers)
    initial_answers = goal_evaluator(goal)

    # 2. Iterate worklist until fixpoint
    while worklist and iterations < max_iterations:
        item = worklist.popleft()
        resume_consumer(item, goal_evaluator)

    # 3. Return final complete answer set
    return table_manager.get_answers(goal_key)

Critical for: Ensuring completeness through systematic exploration.

---

Evidence of the Transition

Code Evolution

Constants File Shows the Struggle

# engine/constants.py

# LEGACY HEURISTICS (kept for fallback):
MAX_EVAL_DEPTH = 100           # “Sufficient for most knowledge bases” (not all!)
MAX_TRANSITIVE_DEPTH = 20      # “Increased... to handle murder mystery scenarios”
MAX_CONSECUTIVE_FAILURES = 10  # “extremely unlikely” - probabilistic reasoning

# NEW CORRECTNESS-FIRST APPROACH:
ENABLE_TABLING = True          # “correct, industry-standard solution”

The comments reveal the shift in philosophy: from “sufficient for most” to “correct for all.”

Test Suite Growth

The tabling test suite shows comprehensive coverage of edge cases:

tests/engine/tabling/test_tabling.py:
- 54 tests (17 → 54 in enhancement, 218% increase)
- TestVariantKeyDeeper: Alpha-equivalence edge cases
- TestTableManagerContracts: Contract enforcement
- TestCyclesVsNonCycles: Correct cycle vs non-cycle discrimination
- TestResultCleaning: User-facing API guarantees

These tests codify lessons learned from counter-based failures.

Derived Evaluator Refactoring

The DerivedEvaluator class still maintains legacy cycle detection as a fallback, showing the cautious migration:

# engine/derived_evaluator.py:55-60
# Recursion depth tracking
self._eval_depth = 0
self._max_eval_depth = 100

# Query cycle detection
self._eval_stack: Set[Tuple[str, str]] = set()

This defensive layering suggests the team learned: don’t trust heuristics alone.

---

The Architectural Lessons

1. Heuristics Hide Correctness Bugs

Counter-based limits appear to work because:

• Most queries don’t hit the limits

• Failures are subtle (incomplete results, not crashes)

• Edge cases occur infrequently

Lesson: Probabilistic heuristics are appropriate for optimization, not correctness.

2. Adjustable Limits Are a Warning Sign

Every time a limit needed adjustment (MAX_TRANSITIVE_DEPTH: 10 → 20), it signaled that the approach was fighting the problem, not solving it.

Lesson: If you keep tuning a parameter to handle new cases, you need a different algorithm.

3. Workarounds Compound Complexity

The temporary eval stack clearing (saved_stack = self._eval_stack.copy()) was a workaround to fix a workaround. This created:

• Subtle interactions between subsystems

• Hard-to-debug state management issues

• Fragile code requiring deep system knowledge

Lesson: When workarounds accumulate, it’s time to re-architect.

4. Industry Standards Exist for a Reason

Tabling has been the standard solution in Prolog systems (XSB, SWI-Prolog) for decades because:

• The correctness properties are provable

• The performance characteristics are well-understood

• Edge cases have been thoroughly explored

Lesson: Don’t reinvent the wheel - especially for hard problems like recursion handling.

---

The Path Forward: Tabling Integration

Current State (as of October 2025)

The system now has dual-mode evaluation:

# engine/constants.py
ENABLE_TABLING = True  # Default: use table-based approach

When tabling is enabled:

1. Recursive queries use producer/consumer protocol

2. Variant matching provides cycle detection

3. Fixpoint iteration ensures completeness

4. Legacy counters remain as defensive backstops

Migration Strategy

The team chose gradual migration rather than a flag-day cutover:

1. Phase 1 (Complete): Implement tabling infrastructure

   • Variant key system

   • Table manager

   • Fixpoint driver

   • Comprehensive test suite

2. Phase 2 (In Progress): Route queries to appropriate engine

   • Recursive predicates → Tabling

   • Temporal queries → Legacy (for now)

   • Simple queries → Either (performance)

3. Phase 3 (Future): Deprecate counter-based heuristics

   • Remove MAX_CONSECUTIVE_FAILURES

   • Simplify depth limits to stack protection only

   • Clean up eval stack workarounds

Performance Considerations

Tabling trades memory for correctness and speed:

Memory: Tables store intermediate results

• Mitigation: Per-query table clearing, LRU eviction policies

• Configuration: MAX_TABLE_ANSWERS_PER_VARIANT (currently unlimited)

Speed: Memoization eliminates redundant computation

• Benefit: Queries that previously hit depth limits now complete instantly

• Example: path(a, X) on a 1000-node graph completes in constant time on second call

---

Conclusion: From Heuristics to Principled Design

The recursion bug was not a single coding error - it was a fundamental architectural issue. Counter-based heuristics were:

• Reasonable as a first approach

• Effective for common cases

• Insufficient for correctness guarantees

The evolution to table-based solution represents:

• Recognition that heuristics cannot replace algorithms

• Adoption of industry-proven techniques

• Investment in long-term correctness over short-term simplicity

Key Takeaway for Future Development

When building a reasoning system:

• Don’t: Rely on adjustable limits for correctness

• Don’t: Accumulate workarounds for edge cases

• Do: Use proven algorithms from the literature

• Do: Design for completeness and termination from the start

The recursive query problem is solved in the tabling literature. The BSF2-IF system’s journey from custom heuristics to SLG-style tabling is a case study in recognizing when to adopt proven solutions rather than reinventing them.

---

References and Further Reading

Implementation Files

• src/kb/engine/constants.py - Configuration and limits (shows historical evolution)

• src/kb/engine/tabling/table_manager.py - Producer/consumer protocol

• src/kb/engine/tabling/fixpoint_driver.py - Fixpoint iteration algorithm

• src/kb/engine/tabling/variant_key.py - Variant matching and normalization

• src/kb/tests/engine/tabling/test_tabling.py - Comprehensive test suite (54 tests)

Academic Literature

• Chen & Warren (1996): “Tabled Evaluation with Delaying” - Foundational SLG paper

• Swift & Warren (2012): “XSB: Extending Prolog with Tabled Logic Programming”

• Wielemaker et al. (2020): “Tabling in SWI-Prolog” - Modern implementation